目的

缩小图像（或称为下采样（subsampled）或降采样（downsampled））的主要目的：

1、使得图像符合显示区域的大小；

2、生成对应图像的缩略图。

放大图像（或称为上采样（upsampling）或图像插值（interpolating））的主要目的是放大原图像,从而可以显示在更高分辨率的显示设备上。

对图像的缩放操作并不能带来更多关于该图像的信息, 因此图像的质量将不可避免地受到影响。然而，确实有一些缩放方法能够增加图像的信息，从而使得缩放后的图像质量超过原图质量的。

原理

下采样原理：对于一幅图像I尺寸为MN，对其进行s倍下采样，即得到(M/s)(N/s)尺寸的得分辨率图像，当然s应该是M和N的公约数才行，如果考虑的是矩阵形式的图像，就是把原始图像s*s窗口内的图像变成一个像素，这个像素点的值就是窗口内所有像素的均值：

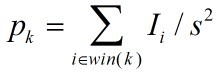
上采样原理：图像放大几乎都是采用内插值方法，即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。

插值算法分类

对插值算法分类比较混乱，各人有各人的分类算法。文献《图像插值技术综述》中简略的将插值算法分为传统插值、 基于边缘的插值和基于区域的插值3类，作为初学者入门明晰插值算法还是有帮助。

1.传统差值原理和评价

在传统图像插值算法中，邻插值较简单，容易实现，早期的时候应用比较普遍。但是，该方法会在新图像中产生明显的锯齿边缘和马赛克现象。双线性插值法具有平滑功能，能有效地克服邻法的不足，但会退化图像的高频部分，使图像细节变模糊。在放大倍数比较高时，高阶插值，如双三次和三次样条插值等比低阶插值效果好。这些插值算法可以使插值生成的像素灰度值延续原图像灰度变化的连续性，从而使放大图像浓淡变化自然平滑。但是在图像中，有些像素与相邻像素间灰度值存在突变，即存在灰度不连续性。这些具有灰度值突变的像素就是图像中描述对象的轮廓或纹理图像的边缘像素。在图像放大中，对这些具有不连续灰度特性的像素，如果采用常规的插值算法生成新增加的像素，势必会使放大图像的轮廓和纹理模糊，降低图像质量。

2.基于边缘的图像插值算法

为了克服传统方法的不足， 提出了许多边缘保护的插值方法，对插值图像的边缘有一定的增强， 使得图像的视觉效果更好， 边缘保护的插值方法可以分为两类： 基于原始低分辨图像边缘的方法和基于插值后高分辨率图像边缘的方法。基于原始低分辨率图像边缘的方法:( 1)首先检测低分辨率图像的边缘， 然后根据检测的边缘将像素分类处理， 对于平坦区域的像素，采用传统方法插值；对于边缘区域的像素， 设计特殊插值方法， 以达到保持边缘细节的目的。(2)基于插值后高分辨率图像边缘的方法这类插值方法:首先采用传统方法插值低分辨率图像，然后检测高分辨率图像的边缘，最后对边缘及附近像素进行特殊处理， 以去除模糊， 增强图像的边缘。

3.基于区域的图像插值算法

首先将原始低分辨率图像分割成不同区域，然后将插值点映射到低分辨率图像， 判断其所属区域， 最后根据插值点的邻域像素设计不同的插值公式， 计算插值点的值。

CNN中的池化操作

采样层是使用 pooling的相关技术来实现的，目的就是用来降低特征的维度并保留有效信息，一定程度上避免过拟合。但是pooling的目的不仅仅是这些，他的目的是保持旋转、平移、伸缩不变形等。

采样有最大值采样，平均值采样，求和区域采样和随机区域采样等。池化也是这样的，比如最大值池化，平均值池化，随机池化，求和区域池化等。

• mean-pooling，即对邻域内特征点只求平均，
• max-pooling，即对邻域内特征点取最大。

根据相关理论，特征提取的误差主要来自两个方面：（1）邻域大小受限造成的估计值方差增大；（2）卷积层参数误差造成估计均值的偏移。一般来说，mean-pooling能减小第一种误差，更多的保留图像的背景信息，max-pooling能减小第二种误差，更多的保留纹理信息。

• Stochastic-pooling则介于两者之间，通过对像素点按照数值大小赋予概率，再按照概率进行亚采样，再平均

来源: